Bypass and Decoupling Capacitors--Some Thoughts and Modeling

Wes Hayward, w7zoi  4 Sept 2019.

A recent on-line post asked about the practices that we used with circuits in the book Experimental Methods in RF Design.   The question asked about the decoupling resistors used and how the values were determined.   This is a subject that I often encounter and I thought it would be worth further  discussion.

Let's start with a common circuit, a two stage amplifier.   Both stages are identical, but the component values are usually different.   There is nothing special about this circuit.  It's just a vehicle for our discussion.

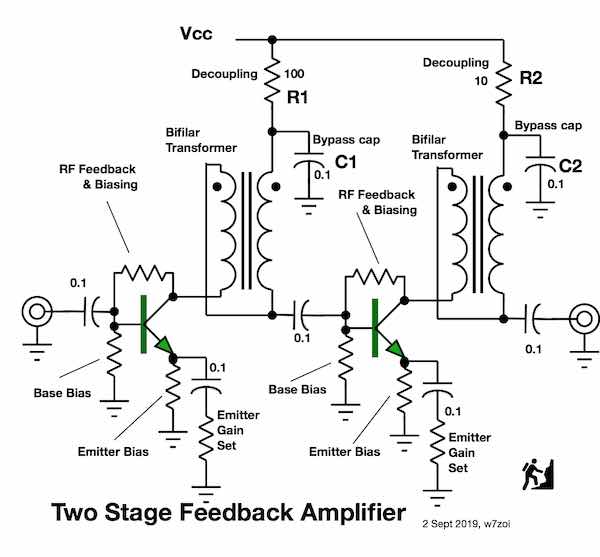  Fig 1.   Each of the two stages in this circuit is decoupled from the power source with a resistor.  R1 is 100 and R2=10 ohms.    The two stages each have power gain, so the signals at the input to the second stage are larger than those at the input to the first stage.   The second stage will probably be biased for more current, so that decoupling resistor, R2, must be lower.     The decoupling element is part of the overall bias and must be taken into account during bias design.

Let's back away from the application shown in Fig 1 and concentrate on just one stage, and specifically, on one of the bypass capacitors, C1.   The value for this part is 0.1 uF, certainly a popular and common part.   This component has two functions.   First, as a bypass, it establishes the AC potential at zero.   The capacitor will, of course, have a DC present from the bias, but will force the AC signal voltage toward zero.    Recall that a capacitor is an element that resists a change in voltage, just as an inductor impedes a change in current.    

Assume that capacitor C1 is perfect.  We'll discuss imperfections later.     So, how effective is C1 in attenuating noise or signals that might be on the power supply buss, assuming no decoupling resistor?     The power supply is not perfect.   That is, it has a finite output impedance that may well be a function of frequency.     Assume for this example that the power supply has an output resistance of 1 ohm.      The behavior of C1 is then shown in Fig. 2 below, a SPICE calculation of the response of the filter formed by the 1 ohm power supply resistance and C1.  
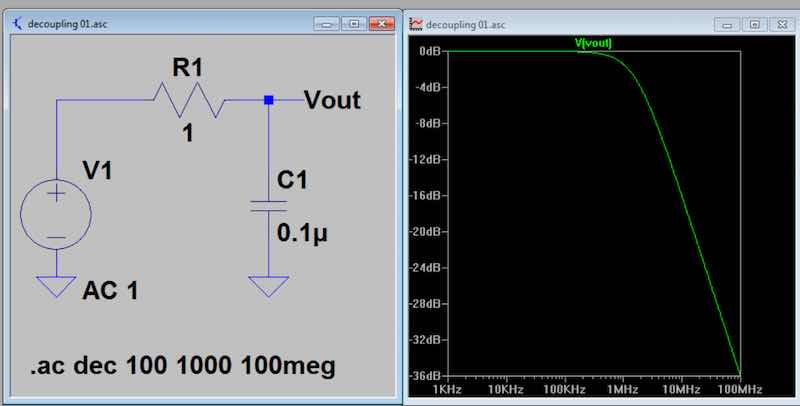Fig 2.   This circuit produces the response in the related curve.   The response can be used to calculate the impedance (magnitude) of the capacitor versus frequency.   

The reactance of the 0.1 uF capacitor can be calculated directly.   This is shown in the following table.

F                Xc
1 kHz        1591  ohm
1 MHz       1.59
10 MHz     0.16
100 MHz    .016 

What happens if we now include 10 or 100 ohm resistors?    These are compared with the 1 ohm response in Fig 3.
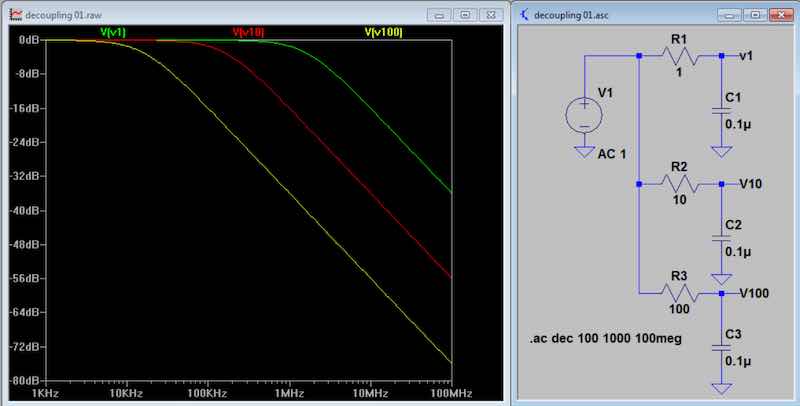Fig 3.   Response with various values of resistance in the single element low pass filter.   (It is just a single filter that is analyzed three times.)    A change in R by 10 yields a 20 dB improvement in attenuation of power supply noise at the capacitor.  C1 is assumed to be perfect.    Note that all three plots have the same slope of 6 dB/octave or 20 dB per decade. 

Now for some reality.   If a capacitor is studied with a network analyzer, a strong resonance is observed in almost all cases.   This is the result of so called lead length inductance resonating with the capacitance.     The term lead length is something of a misnomer, for even SMT parts with zero lead length will show this resonance.    As it turns out, all that is required to obtain an effective inductance is the physical length of the capacitor. 
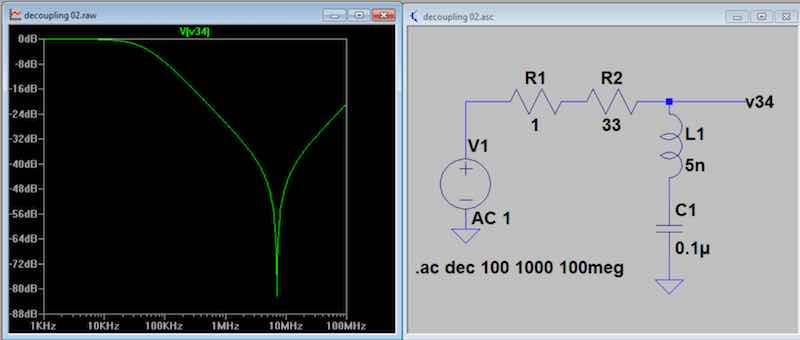Fig 4.   This plot models the capacitor as a series LC where the C is the low frequency measured value of 0.1 uF and the L is commensurate with the length.   A reasonable inductance constant is 10 nH/cm.   The best way to get the L parameter though is to measure it.   Measure the resonant frequency and calculate L on the basis of the marked capacitance.    (Remember Kopski's rule:  TMITK, or "To Measure is to Know.)    This example uses a 33 ohm decoupling resistor.   The slope of the response and the frequency where it starts to depart from the zero attenuation by a dB or so are the same as the the earlier examples when R is taken into account.    The resonance for this example is 7 MHz.   

There is some virtue to this resonance.   There are some applications where it is desirable to get a very good bypass or good decoupling at one specific frequency.    However, in most cases, we want good wide band performance.

The previous example used a 0.1 uF capacitor with a stray L of 5 nH.    The next example considers a 1000 pF capacitance with stray L of 2 nH. 
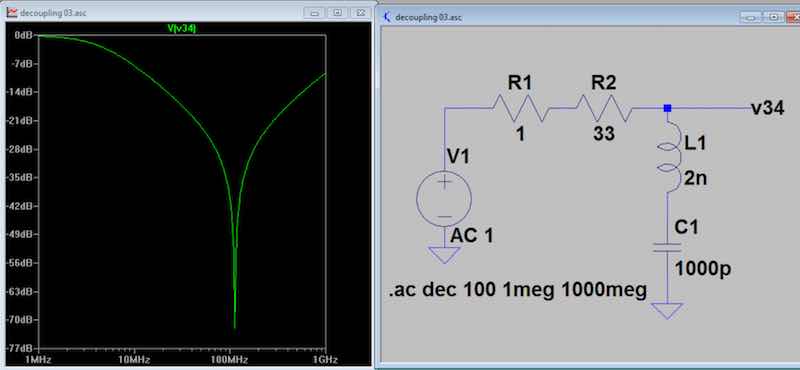Fig 5.    The frequency sweep is repeated, but over a wider bandwidth.   This part resonates at 114 MHz.   The response away from the dip is like the simpler parts.  

This is where things get embarrassing:    Back in the 1970s, lore among RF folks was that a good way to enhance wide band decoupling was to use parallel capacitors of differing value.   Combinations of 3 or more were common, with a common set being 0.1 uF, .01 uF, and 1000 pF.    Sometimes additional parts were added.    The following Fig 6 shows what happens with the parallel combination of a 0.1 uF and 1000 pF, the two capacitors just analyzed.
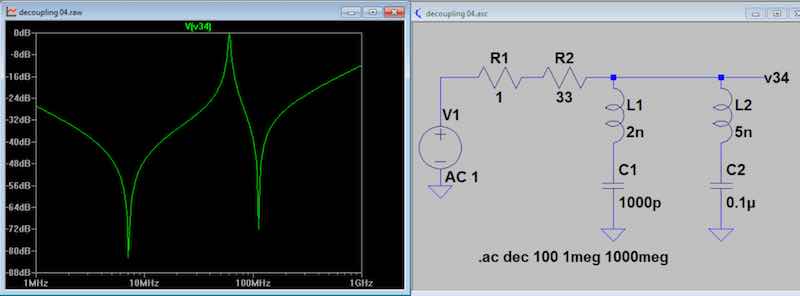  Fig 6.  A second tuned LC is added to the first bypass capacitor, generating the predicted second dip.    The overall response values are -82 dB at 7 and -72 dB at 112 MHz.   But there is a major problem:  the attenuation is less than 1 dB at 60 MHz!    This could be a really big problem in some circuits.   At that frequency, there is virtually no decoupling or bypassing at all.    The circuit using this quasi bypass would operate as if there was no bypass at all at that frequency.    How many cases of stray oscillation can be explained by this; I can think of some.    Note that parallel resonance happens where the 1000 pF resonates with the total L of both elements, 7 nH.   

Embarrassment was mentioned above.   In my 1982 book, Introduction to RF Design (Prentice-Hall, 1982), page 13, I repeated the lore of the day regarding the parallel unequal capacitors.   Clearly, this was an error.  I had completely forgotten about this statement.    I do remember colleagues blowing a hole in this lore sometime at about 1990 when I was working at TriQuint Semiconductor. 

The next example adds one more capacitor to the mix, a .01 uF with stray L of 3 nH.
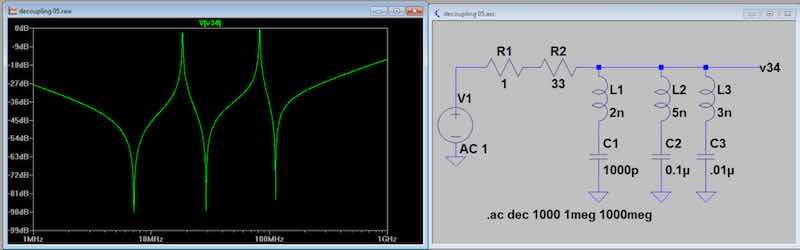  Fig 7.   Three capacitors are paralleled to produce three series frequencies of high attenuation, but two undesired intermediate frequencies of almost no filtering.     

When Rick Campbell and Bob Larkin and I were putting Experimental Methods in RF Design (ARRL, 2003) together, I started to write the same old lore.   It had been around so long that I started to believe it.     But Bob caught it.   Moreover, he was experienced in these things and knew to point me in a direction that actually works.    Figure 8 below shows what happens when three capacitors of EQUAL value are used for a bypass.  In this case, three .01 uF caps, each with L=3 nH are paralleled.
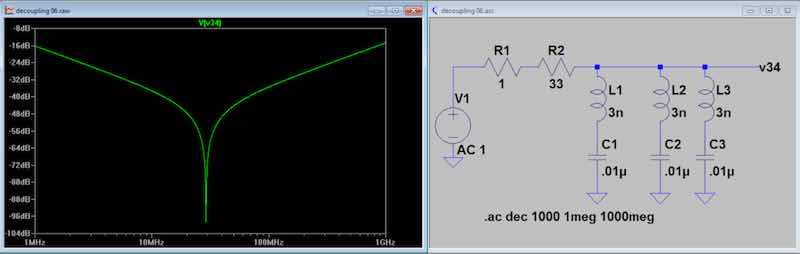Fig 8.  Three identical capacitors produce a very deep null at resonance, but do not generate an offensive parallel resonance.   

It only gets better as more capacitors are added.   The figure below shows the response with 7 identical parallel capacitors.
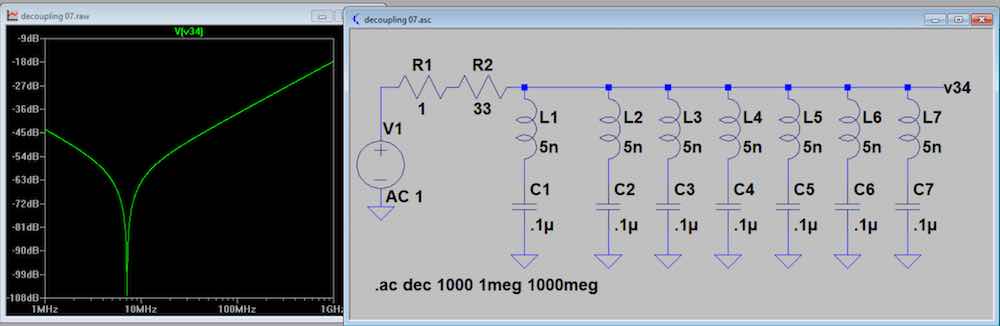  Fig 9.   This example is much like the previous case, but the .01 uF caps are replaced by seven 0.1 uF units with 5 nH stray L.  Again, no stray parallel responses are seen.

We often see designs where stages are bypassed, but there is no decoupling.   That is, R1 and R2 of Fig 1 are eliminated.    Sometimes the circuit works, but sometimes it does not and there may be no obvious reason.       The following schematic illustrates this.    When the amplifiers of Fig 1 uses no decoupling resistors, the two 0.1 uF bypass caps are then paralleled, resulting in the 0.2 uF capacitor of Fig 10.   The increased C value has little impact.    The larger problem, one that has major impact is that the two stages are now tightly coupled to each other.     Any signal at one amplifier might generate a voltage across the bypass.   But that signal is now available, without attenuation, to the bypass capacitor node of the other stage.    After all, those two nodes are one and the same.  The problem is potentially even worse.     C1 of Fig 1 spans from the transformer power supply end to ground.   The same argument applies to C2 in the second stage of Fig 1.   The grounds are different.   They may even be in different shielded enclosures.      When the decoupling resistors disappear, the two capacitors become one and all ground signals in one stage are now shared with the other.
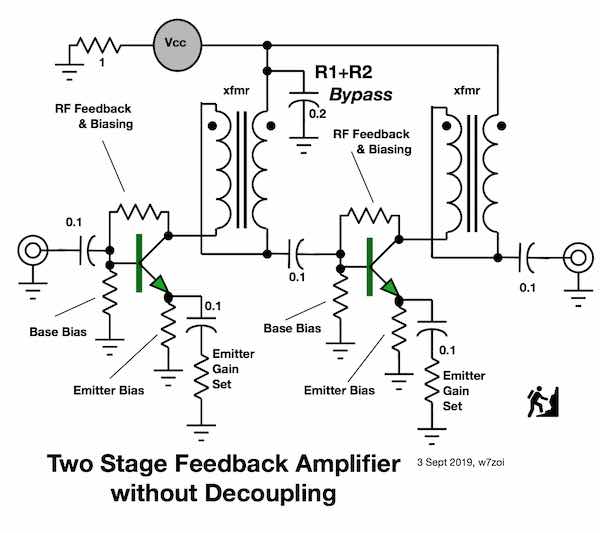Fig 10.  This circuit illustrates the problem sometimes encountered when decoupling resistor for each stage are eliminated.  

We should elaborate by what is intended when we say that a design "does not work."    In the extreme, there may be an oscillation, an obvious problem.   But the more common dysfunction is more subtle.   The gain may be more or less than we sought in our design.   This can be especially frustrating in measurement equipment.    Even more insidious, the distortion may be out of line.    It is important in a careful design to simulate these things and then to measure them and compare the results.    

The analysis so far has examined the signal (or noise) from the power supply that might end up at one of the amplifier stages.      The decoupling also operates in the other direction.    Envision Fig 1 where a signal source is now placed in parallel with C1.   This emulates a signal that may be in the first stage.   A small resistance (R1, below) is included with the source.   Voltage sources don't play well with lossless reactive terminations in SPICE.    We wish to evaluate the strength of this signal when it reaches the supply.   The power supply itself serves as a load for this signal.   This analysis is shown in Fig 11 below.
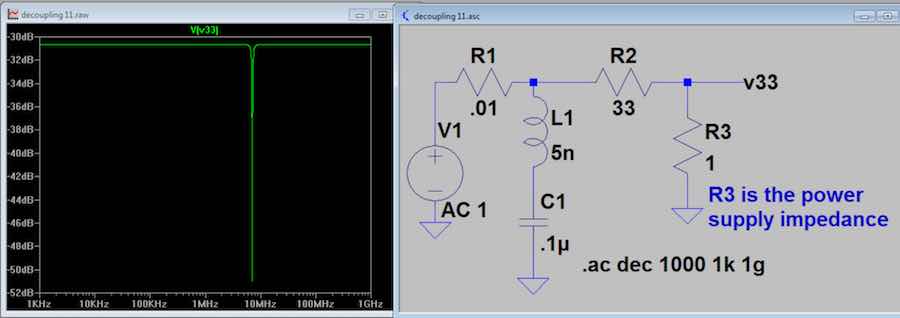Fig 11.   A 33 ohm decoupling resistor acts against the power supply internal 1 ohm impedance to provide a 31 dB attenuation at the supply for signals originating within the amplifier.     Dropping the decoupling R to 5 ohms reduces the attenuation to 16 dB.

Loss can alter the results.   This is easily modeled with the insertion of series resistance in the "capacitor" series LC model.  
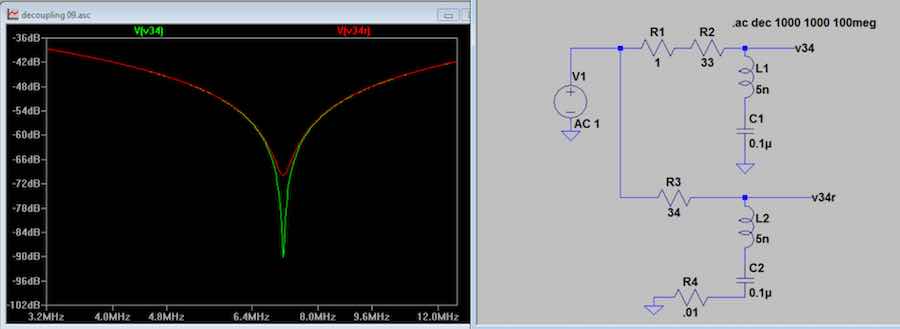Fig 12.  This plot is just a repeat of Fig 4 except that a second circuit variant is added that includes a .01 ohm series resistance.   That response is shown in red.    Loss has minimal impact except when examining the depth of the notch related to the capacitor series resonance.

Quite a bit of discussion has been devoted to the use of parallel capacitors.    A rule emerges--only use them when the caps are of equal value.   One possible exception to the recommendation to avoid unequal caps has to do with an added electrolytic capacitor.    In one experiment, I had measured a filtering decoupling network, much like Fig 4, and then added a 100 uF aluminum electrolytic.   It was nothing special, but just one of the routine parts that we use.    The measurement was repeated.    The performance at RF changed by no more than 1 dB over the HF band of interest.   The low frequency decoupling was improved.

Concluding Thoughts

Any stage in a system, be it a transmitter, a receiver, or a complete transceiver, will have several stages.    These will all require at least one bypass capacitor.   Often, the bypass is also part of a decoupling network that routes to a power supply or a control signal.    A viable rule is that a bypass for one stage  should never be shared with a second stage.   Moreover. each line that leave the stage should be through an impedance.   If a resistor is not desired, an RFC can sometimes be used.   Sometime it is necessary to join several of these supply lines together in a bypass capacitor.   An example might be a feed through capacitor where several stage within a shielded enclosure reside.   It may then be useful to add an impedance after the common shunt capacitor. 

I've often done transceivers where the only stage that is connected directly to the power supply is the output power amplifier.   Every other stage attaches to the power supply with a series impedance.

There is a school of folks who will build a rig, and will then start removing parts with the hope that the rig will continue to function.   I don't embrace this approach.

Finally, it is interesting to look at an exercise like the one I just went through and to attribute it to our modern conveniences.   We all have some reasonable measurement equipment, with a 50 MHz oscilloscope as a minimum.    And we all have a compute with free software that does all sorts of interesting, fun stuff for us.    I used LT SPICE for this effort.   (Thanks to Linear Technology, now part of Analog Devices.)    But none of this analysis required any of this sophistication.   All analysis was linear and could be done with a programmable hand calculator.   Indeed, it could probably have been done with paper and slide rule, although it would get pretty tedious.